Orbita ellittica

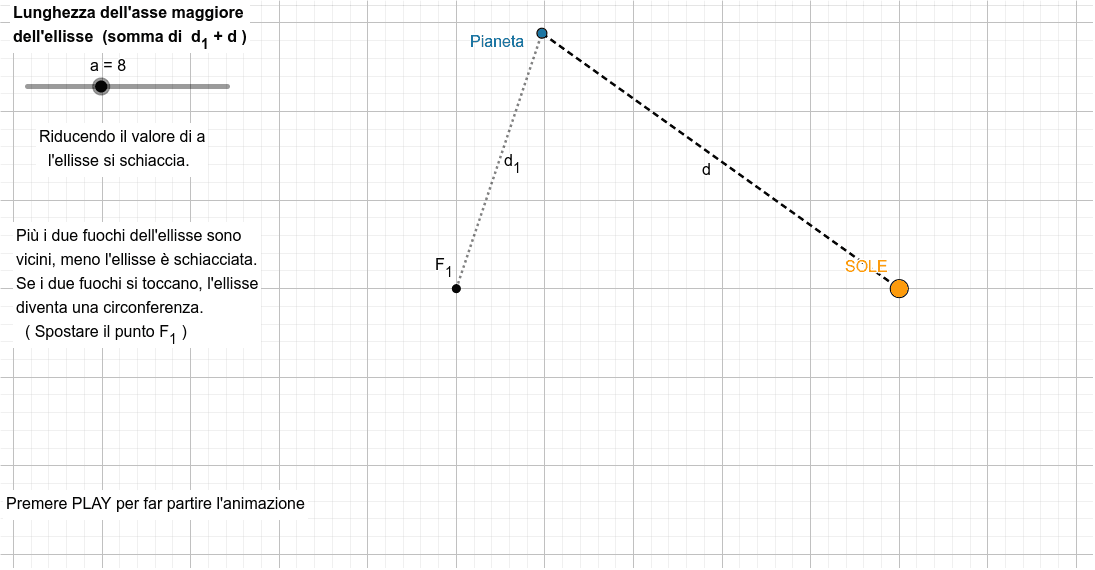
In astrodinamica e in meccanica celeste un'orbita ellittica è un'orbita con eccentricità maggiore di 0 e minore di 1.

L'energia specifica di un'orbita ellittica è negativa.

Velocità

Sotto le ipotesi standard la velocità orbitale di un corpo che si muove su un'orbita ellittica può essere calcolata come:

${\displaystyle v={\sqrt {2\mu \left({1 \over {r}}-{1 \over {2a}}\right)}}}$

dove:

• ${\displaystyle \mu }$ è la costante gravitazionale planetaria,
• ${\displaystyle r}$ è il raggio dell'orbita equivalente alla distanza radiale del corpo orbitante calcolata a partire dal centro del corpo stesso,
• ${\displaystyle a}$ è la lunghezza del semiasse maggiore.

Periodo orbitale

Sotto le ipotesi standard il periodo orbitale di un corpo che si muove su un'orbita ellittica può essere calcolato come:

${\displaystyle T={2\pi \over {\sqrt {\mu }}}a^{3 \over {2}}}$

dove:

• ${\displaystyle \mu }$ è la costante gravitazionale planetaria,
• ${\displaystyle a}$ è la lunghezza del semiasse maggiore.

Conclusioni:

• il periodo orbitale corrisponde a quello di un'orbita circolare con raggio pari al semiasse maggiore (${\displaystyle a}$),
• il periodo orbitale non dipende dall'eccentricità.

Energia

Sotto le ipotesi standard, l'energia orbitale specifica (${\displaystyle \epsilon }$) di un'orbita ellittica è negativa e l'equazione della conservazione dell'energia per quest'orbita prende la forma:

${\displaystyle {v^{2} \over {2}}-{\mu \over {r}}=-{\mu \over {2a}}=\epsilon <0}$

dove:

• ${\displaystyle v}$ è la velocità orbitale del corpo orbitante,
• ${\displaystyle r}$ è la distanza radiale del corpo orbitante dal centro del corpo centrale,
• ${\displaystyle a}$ è la lunghezza del semiasse maggiore.
• ${\displaystyle \mu }$ è la costante gravitazionale planetaria.

Conclusioni:

• L'energia specifica per le orbite ellittiche è indipendente dall'eccentricità ed è funzione del solo semiasse maggiore dell'ellisse.

Dal teorema del viriale si ottiene che:

• la media temporale dell'energia potenziale specifica è uguale a 2ε
• la media temporale di r^-1 coincide con a^-1
• la media temporale dell'energia cinetica specifica è uguale a -ε

Sistema solare

Nel sistema solare i pianeti, gli asteroidi, le comete e i detriti spaziali hanno orbite ellittiche attorno al Sole.

Le lune hanno orbite ellittiche attorno ai loro pianeti.

Molti satelliti artificiali hanno diverse orbite ellittiche attorno alla Terra.

Note

Bibliografia

• (EN) Richard H. Battin, An Introduction to the Mathematics and Methods of Astrodynamics, AIAA, 1999, ISBN 9781600860263.
• (EN) Vladimir A. Chobotov, Orbital Mechanics, 3ª ed., AIAA, 2002, ISBN 9781600860973.
• (EN) Howard D. Curtis, Orbital Mechanics for Engineering Students, 3ª ed., Butterworth-Heinemann, 2013, ISBN 978-0-08-097747-8.
• Giovanni Mengali e Alessandro Quarta, Fondamenti di Meccanica del Volo Spaziale, Pisa, Plus - Pisa University Press, 2006, ISBN 978-88-8492-413-1.
• (EN) David A. Vallado, Fundamentals of Astrodynamics and Applications, 2ª ed., Springer Science & Business Media, 2001, ISBN 9780792369035.

Voci correlate

• Leggi di Keplero
• Orbita
• Orbita circolare
• Traiettoria parabolica
• Traiettoria iperbolica